Нет, они не одинаковы. Если машинное обучение — это просто прославленная статистика, то архитектура — это просто прославленное строительство песчаных замков.
Я, честно говоря, устал от повторения этой дискуссии в социальных сетях и в моем университете почти ежедневно.
Обычно это сопровождается довольно расплывчатыми заявлениями, чтобы объяснить проблему. Обе стороны виноваты в этом.
Я надеюсь, что к концу этой статьи у вас будет более информированная позиция по этим несколько расплывчатым терминам.
Аргумент
Вопреки распространенному мнению, машинное обучение существует уже несколько десятилетий.
Первоначально его избегали из-за его больших вычислительных требований и ограничений вычислительной мощности, существующих в то время.
Тем не менее, в последние годы в машинном обучении наблюдается оживление благодаря преобладанию данных, полученных в результате информационного взрыва.
Итак, если машинное обучение и статистика являются синонимами друг друга, почему мы не видим, чтобы каждый отдел статистики в каждом университете закрывался или переходил в отдел «машинного обучения»?
Потому что они не одинаковы!
Есть несколько расплывчатых утверждений, которые я часто слышу по этой теме, наиболее распространенным из которых является что-то вроде этого:
«Основное различие между машинным обучением и статистикой — это их цель.
Модели машинного обучения предназначены для максимально точных прогнозов. Статистические модели предназначены для вывода о взаимосвязи между переменными».
Хотя это технически верно, это не дает особенно явного или удовлетворительного ответа.
Основное различие между машинным обучением и статистикой — действительно их цель.
Однако говорить, что машинное обучение — это все о точных предсказаниях, в то время как статистические модели, разработанные для умозаключений, является почти бессмысленным утверждением, если вы не разбираетесь в этих понятиях.
Во-первых, мы должны понимать, что статистика и статистические модели не совпадают. Статистика — это математическое исследование данных.
Вы не можете делать статистику, если у вас нет данных.
Статистическая модель — это модель для данных, которая используется либо для вывода чего-либо об отношениях внутри данных, либо для создания модели, способной прогнозировать будущие значения.
Часто эти двое идут рука об руку.
Таким образом, на самом деле нам нужно обсудить две вещи: во-первых, как статистика отличается от машинного обучения, и, во-вторых, как статистические модели отличаются от машинного обучения.
Чтобы сделать это немного более явным, существует множество статистических моделей, которые могут делать прогнозы, но точность прогноза не в их силе.
Аналогичным образом, модели машинного обучения обеспечивают различную степень интерпретируемости, от легко интерпретируемой регрессии лассо до непроницаемых нейронных сетей, но они, как правило, жертвуют интерпретируемостью для предсказательной силы.
С точки зрения высокого уровня, это хороший ответ. Достаточно хорошо для большинства людей.
Однако есть случаи, когда это объяснение оставляет у нас неправильное понимание различий между машинным обучением и статистическим моделированием.
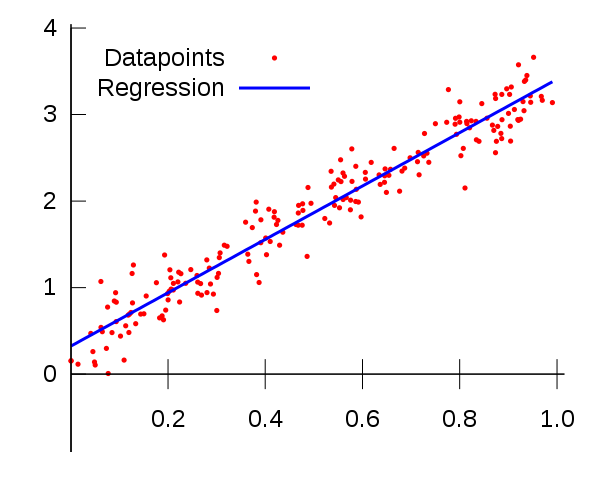
Давайте посмотрим на пример линейной регрессии.
Статистические модели против машинного обучения — пример линейной регрессии
Мне кажется, что сходство методов, используемых в статистическом моделировании и в машинном обучении, заставило людей предположить, что это одно и то же.
Это понятно, но просто не соответствует действительности.
Наиболее очевидным примером является случай линейной регрессии, которая, вероятно, является основной причиной этого недоразумения.
Линейная регрессия — это статистический метод, мы можем обучить линейный регрессор и получить тот же результат, что и модель статистической регрессии, чтобы минимизировать квадратичную ошибку между точками данных.
Мы видим, что в одном случае мы делаем то, что называется «обучением» модели, которая включает использование подмножества наших данных, и мы не знаем, насколько хорошо будет работать модель, пока мы не «проверим» эти данные на дополнительных данных, которых не было, во время тренировки называется тестовый набор.
Цель машинного обучения, в данном случае, состоит в том, чтобы получить наилучшую производительность на тестовом наборе.
Для статистической модели мы находим линию, которая минимизирует среднеквадратичную ошибку для всех данных, предполагая, что данные являются линейным регрессором с добавлением некоторого случайного шума, который обычно имеет гауссовский характер.
Не требуется никаких тренировок и тестов. Во многих случаях, особенно в исследованиях (таких как пример датчика ниже), цель нашей модели состоит в том, чтобы охарактеризовать взаимосвязь между данными и нашей конечной переменной, а не делать прогнозы относительно будущих данных.
Мы называем эту процедуру статистическим выводом, а не прогнозированием.
Тем не менее, мы все еще можем использовать эту модель для прогнозирования, и это может быть вашей основной целью, но способ оценки модели не будет включать набор тестов, а вместо этого будет включать оценку значимости и надежности параметров модели.
Целью (контролируемого) машинного обучения является получение модели, которая может делать повторяющиеся прогнозы.
Нам, как правило, не важно, интерпретируется ли модель, хотя я лично рекомендую всегда тестировать, чтобы убедиться, что предсказания модели действительно имеют смысл.
Машинное обучение — это все о результатах, оно, вероятно, работает в компании, где ваша ценность характеризуется исключительно вашей успеваемостью.
Принимая во внимание, что статистическое моделирование больше связано с поиском взаимосвязей между переменными и значимостью этих взаимосвязей, а также с предсказанием.
Чтобы привести конкретный пример различия между этими двумя процедурами, я приведу личный пример. Днем я ученый-эколог и работаю в основном с данными датчиков.
Если я пытаюсь доказать, что датчик способен реагировать на определенный тип раздражителей (например, концентрацию газа), то я бы использовал статистическую модель, чтобы определить, является ли отклик сигнала статистически значимым.
Я хотел бы попытаться понять это соотношение и проверить его повторяемость, чтобы я мог точно характеризовать реакцию датчика и делать выводы на основе этих данных.
Некоторые вещи, которые я мог бы проверить, являются ли реакция, на самом деле, линейной, можно ли реагировать на концентрацию газа, а не на случайный шум в датчике и т.д.
Напротив, я также могу получить массив из 20 различных датчиков, и я могу использовать это, чтобы попытаться предсказать реакцию моего недавно охарактеризованного датчика.
Это может показаться немного странным, если вы мало знаете о датчиках, но в настоящее время это важная область науки об окружающей среде.
Модель с 20 различными переменными, предсказывающими результат работы моего датчика, явно относится к прогнозированию, и я не ожидаю, что он будет особенно интерпретируемым.
Эта модель, вероятно, будет чем-то более эзотерическим, как нейронная сеть, из-за нелинейностей, возникающих из-за химической кинетики и взаимосвязи между физическими переменными и концентрациями газа.
Я хотел бы, чтобы модель имела смысл, но пока я могу делать точные прогнозы, я был бы очень счастлив.
Если я пытаюсь доказать связь между моими переменными данных до степени статистической значимости, чтобы я мог опубликовать ее в научной статье, я использовал бы статистическую модель, а не машинное обучение.
Это потому, что меня больше интересует взаимосвязь между переменными, а не прогнозирование.
Прогнозы все еще могут быть важны, но отсутствие интерпретируемости, присущей большинству алгоритмов машинного обучения, затрудняет доказательство взаимосвязей в данных (на самом деле это большая проблема в научных исследованиях, поскольку исследователи используют алгоритмы, которые они не понимают, и не получают их). ложные умозаключения).
Оценка алгоритма машинного обучения использует набор тестов для проверки его точности.
Принимая во внимание, что для статистической модели анализ параметров регрессии с помощью доверительных интервалов, тестов значимости и других тестов может использоваться для оценки легитимности модели.
Поскольку эти методы дают одинаковый результат, легко понять, почему можно предположить, что они одинаковы.
Статистика против машинного обучения — пример линейной регрессии
Я думаю, что это заблуждение довольно хорошо заключено в эту якобы остроумную 10-летнюю задачу, сравнивающую статистику и машинное обучение.
Однако объединение этих двух терминов, основанных исключительно на том факте, что они оба используют одни и те же фундаментальные понятия вероятности, является неоправданным.
Например, если мы сделаем утверждение, что машинное обучение — это просто прославленная статистика, основанная на этом факте, мы могли бы также сделать следующие утверждения.
Физика — это просто прославленная математика.
Зоология это просто прославленная коллекция марок.
Архитектура это просто прославленное песчано-замковое строительство.
Эти утверждения (особенно последнее) довольно нелепы, и все они основаны на идее объединения терминов, основанных на похожих идеях (каламбур, предназначенный для примера архитектуры).
В действительности, физика построена на математике, это применение математики для понимания физических явлений, присутствующих в реальности.
Физика также включает в себя аспекты статистики, а современная форма статистики обычно строится на основе структуры, состоящей из теории множеств Цермело-Франкеля в сочетании с теорией меры для создания вероятностных пространств.
У них обоих много общего, потому что они имеют сходное происхождение и применяют сходные идеи для логического вывода.
Точно так же архитектура и строительство песчаных замков, вероятно, имеют много общего — хотя я не архитектор, поэтому я не могу дать обоснованное объяснение — но они явно не одно и то же.
Чтобы дать вам представление о том, насколько далеко зашла эта дискуссия, на самом деле в Nature Methods опубликована статья, в которой излагается разница между статистикой и машинным обучением.
Эта идея может показаться смешной, но грустно, что этот уровень обсуждения необходим.
Прежде чем мы продолжим, я быстро проясню два других распространенных заблуждения, связанных с машинным обучением и статистикой.
Это то, что ИИ отличается от машинного обучения, а наука о данных отличается от статистики. Это довольно неоспоримые проблемы, так что это будет быстро.
Data Science — это по существу вычислительные и статистические методы, которые применяются к данным, это могут быть как небольшие, так и большие наборы данных.
Это может также включать такие вещи, как исследовательский анализ данных, где данные анализируются и визуализируются, чтобы помочь ученому лучше понять данные и сделать из них выводы.
Наука о данных также включает такие вещи, как обработка данных и предварительная обработка, и, таким образом, включает в себя некоторый уровень компьютерных наук, поскольку включает в себя кодирование, установку соединений и конвейеров между базами данных, веб-серверами и т. Д.
Вам не обязательно использовать компьютер для ведения статистики, но вы не можете на самом деле заниматься наукой о данных без нее.
Вы можете еще раз увидеть, что хотя наука о данных использует статистику, они явно не совпадают.
Точно так же машинное обучение не то же самое, что искусственный интеллект. Фактически, машинное обучение является подмножеством искусственного интеллекта.
Это довольно очевидно, поскольку мы учим («обучаем») машину делать обобщенные выводы о некотором типе данных на основе предыдущих данных.
Машинное обучение строится на статистике
Прежде чем мы обсудим, что отличает статистику и машинное обучение, давайте сначала обсудим сходства. Мы уже касались этого в предыдущих разделах.
Машинное обучение построено на статистической основе. Это должно быть явно очевидно, поскольку машинное обучение включает в себя данные, и данные должны описываться с использованием статистической структуры.
Однако статистическая механика, которая распространяется на термодинамику для большого числа частиц, также построена на статистической основе.
Понятие давления на самом деле является статистикой, а температура также статистикой.
Если вы думаете, это звучит смешно, достаточно справедливо, но на самом деле это правда. Вот почему вы не можете описать температуру или давление молекулы, это бессмысленно.
Температура — это проявление средней энергии, создаваемой молекулярными столкновениями.
Для достаточно большого количества молекул имеет смысл, что мы можем описать температуру, например, дома или на улице.
Согласитесь ли вы, что термодинамика и статистика одинаковы? Нет, термодинамика использует статистику, чтобы помочь нам понять взаимодействие работы и тепла в форме транспортных явлений.
На самом деле, термодинамика построена на гораздо большем количестве элементов, кроме статистики.
Точно так же машинное обучение опирается на большое количество других областей математики и информатики, например:
1. Теория ML из таких областей, как математика и статистика
2. Алгоритмы ML из таких областей, как оптимизация, матричная алгебра, исчисление
3. Реализации ML на основе компьютерных и технических концепций (например, трюки с ядром, хеширование функций)
Когда кто-то начинает писать код на Python, извлекает библиотеку sklearn и начинает использовать эти алгоритмы, многие из этих концепций абстрагируются, поэтому трудно увидеть эти различия.
В этом случае эта абстракция привела к форме невежества относительно того, что на самом деле включает машинное обучение.
Статистическая теория обучения — Статистические основы машинного обучения
Основное различие между статистикой и машинным обучением заключается в том, что статистика основана исключительно на вероятностных пространствах.
Вы можете получить всю статистику из теории множеств, в которой обсуждается, как мы можем сгруппировать числа в категории, называемые наборами, и затем наложить на этот набор меру, чтобы убедиться, что сумма всех этих значений равна 1.
Мы называем это вероятностью пространство.
Статистика не делает никаких других предположений о вселенной, кроме этих понятий множеств и мер. Вот почему, когда мы указываем пространство вероятностей в очень строгих математических терминах, мы указываем 3 вещи.
Пространство вероятностей, которое мы обозначим так (Ω, F, P), состоит из трех частей:
1. Примерное пространство, Ω, которое является множеством всех возможных результатов.
2. Набор событий F, где каждое событие представляет собой набор, содержащий ноль или более результатов.
3. Присвоение вероятностей событиям P; то есть функция от событий к вероятностям.
Машинное обучение основано на статистической теории обучения, которая все еще основана на этом аксиоматическом понятии вероятностных пространств.
Эта теория была разработана в 1960-х годах и распространяется на традиционную статистику.
Существует несколько категорий машинного обучения, и в связи с этим я сосредоточусь только на контролируемом обучении, поскольку его легче всего объяснить (хотя оно все еще несколько эзотерично, поскольку скрыто в математике).
Статистическая теория обучения для контролируемого обучения говорит нам, что у нас есть набор данных, который мы обозначаем как S = {(xᵢ, yᵢ)}.
Это в основном говорит о том, что мы — набор данных из n точек данных, каждая из которых описывается некоторыми другими значениями, которые мы называем объектами, которые предоставляются x, и эти функции отображаются определенной функцией, чтобы дать нам значение y.
Это говорит о том, что мы знаем, что у нас есть эти данные, и наша цель — найти функцию, которая отображает значения x на значения y.
Мы называем множество всех возможных функций, которые могут описать это отображение как пространство гипотез.
Чтобы найти эту функцию, мы должны дать алгоритму способ «узнать», как лучше всего решить проблему. Это обеспечивается тем, что называется функцией потерь.
Таким образом, для каждой имеющейся у нас гипотезы (предлагаемой функции) нам нужно оценить, как эта функция выполняет, взглянув на значение ожидаемого риска для всех данных.
Ожидаемый риск, по сути, представляет собой сумму функции потерь, умноженную на распределение вероятности данных.
Если бы мы знали совместное распределение вероятностей отображения, было бы легко найти лучшую функцию.
Тем не менее, это в общем случае неизвестно, и поэтому наш лучший выбор — угадать лучшую функцию, а затем эмпирически решить, лучше ли функция потерь или нет.
Мы называем это эмпирическим риском.
Затем мы можем сравнить различные функции и найти гипотезу, которая дает нам минимальный ожидаемый риск, то есть гипотезу, которая дает минимальное значение (называемое инфимумом) всех гипотез в данных.
Тем не менее, алгоритм имеет тенденцию к мошенничеству, чтобы минимизировать его функцию потерь путем подгонки к данным.
Вот почему после изучения функции, основанной на данных обучающего набора, эта функция проверяется на тестовом наборе данных, данных, которых не было в обучающем наборе.
Характер того, как мы только что определили машинное обучение, привел к проблеме переоснащения и обосновал необходимость обучения и тестирования при выполнении машинного обучения.
Это не присуще статистике, потому что мы не пытаемся минимизировать наш эмпирический риск.
Алгоритм обучения, который выбирает функцию, минимизирующую эмпирический риск, называется минимизацией эмпирического риска.
Примеры
Возьмите простой случай линейной регрессии. В традиционном смысле мы стараемся минимизировать ошибку между некоторыми данными, чтобы найти функцию, которую можно использовать для описания данных.
В этом случае мы обычно используем среднеквадратическую ошибку.
Мы выстраиваем это так, чтобы положительные и отрицательные ошибки не отменяли друг друга. Затем мы можем найти коэффициенты регрессии в замкнутой форме.
Так уж получилось, что если мы возьмем нашу функцию потерь как среднеквадратичную ошибку и выполним минимизацию эмпирического риска, как это предусмотрено статистической теорией обучения, мы получим тот же результат, что и традиционный линейный регрессионный анализ.
Это просто потому, что эти два случая эквивалентны, точно так же, как выполнение максимальной вероятности для этих же данных также даст вам тот же результат.
Максимальное правдоподобие имеет другой способ достижения этой же цели, но никто не собирается спорить и говорить, что максимальное правдоподобие такое же, как линейная регрессия.
Простейший случай явно не помогает дифференцировать эти методы.
Еще один важный момент, который следует здесь подчеркнуть, заключается в том, что в традиционных статистических подходах отсутствует концепция обучения и набора тестов, но мы используем метрики, чтобы помочь нам проанализировать, как работает наша модель.
Таким образом, процедура оценки отличается, но оба метода могут дать нам статистически устойчивые результаты.
Еще один момент заключается в том, что традиционный статистический подход дал нам оптимальное решение, потому что решение имело замкнутую форму.
Он не проверял никаких других гипотез и не сходился к решению.
Принимая во внимание, что метод машинного обучения опробовал множество различных моделей и сходился к окончательной гипотезе, которая соответствовала результатам регрессионного алгоритма.
Если бы мы использовали другую функцию потерь, результаты не сходились бы.
Например, если бы мы использовали потерю шарнира (которую нельзя дифференцировать с помощью стандартного градиентного спуска, поэтому потребовались бы другие методы, такие как проксимальный градиентный спуск), тогда результаты не были бы такими же.
Окончательное сравнение может быть сделано с учетом смещения модели.
Можно было бы попросить алгоритм машинного обучения проверить линейные модели, а также полиномиальные модели, экспоненциальные модели и т. Д.,
Чтобы убедиться, что эти гипотезы лучше соответствуют данным, учитывая нашу априорную функцию потерь. Это сродни увеличению пространства соответствующих гипотез.
В традиционном статистическом смысле мы выбираем одну модель и можем оценить ее точность, но не можем автоматически заставить ее выбрать лучшую модель из 100 различных моделей.
Очевидно, что в модели всегда присутствует некоторая погрешность, обусловленная первоначальным выбором алгоритма.
Это необходимо, поскольку поиск произвольной функции, оптимальной для набора данных, является NP-трудной задачей.
Так что лучше?
Это на самом деле глупый вопрос. С точки зрения статистики против машинного обучения, машинное обучение не могло бы существовать без статистики, но машинное обучение очень полезно в современную эпоху из-за обилия данных, к которым человечество имеет доступ после информационного взрыва.
Сравнение машинного обучения и статистических моделей немного сложнее. То, что вы используете, во многом зависит от вашей цели.
Если вы просто хотите создать алгоритм, который может с высокой точностью прогнозировать цены на жилье, или использовать данные, чтобы определить, может ли кто-то заразиться определенными типами заболеваний, лучше всего подходит машинное обучение.
Если вы пытаетесь доказать связь между переменными или делать выводы из данных, статистический подход, вероятно, является лучшим подходом.
Если вы не обладаете достаточным опытом в области статистики, вы все равно можете изучать машинное обучение и использовать его, абстракция, предлагаемая библиотеками машинного обучения, позволяет довольно легко использовать их в качестве неэкспертного специалиста, но вам все равно нужно некоторое понимание основополагающие статистические идеи с целью предотвращения переоснащения моделей и предоставления ложных выводов.

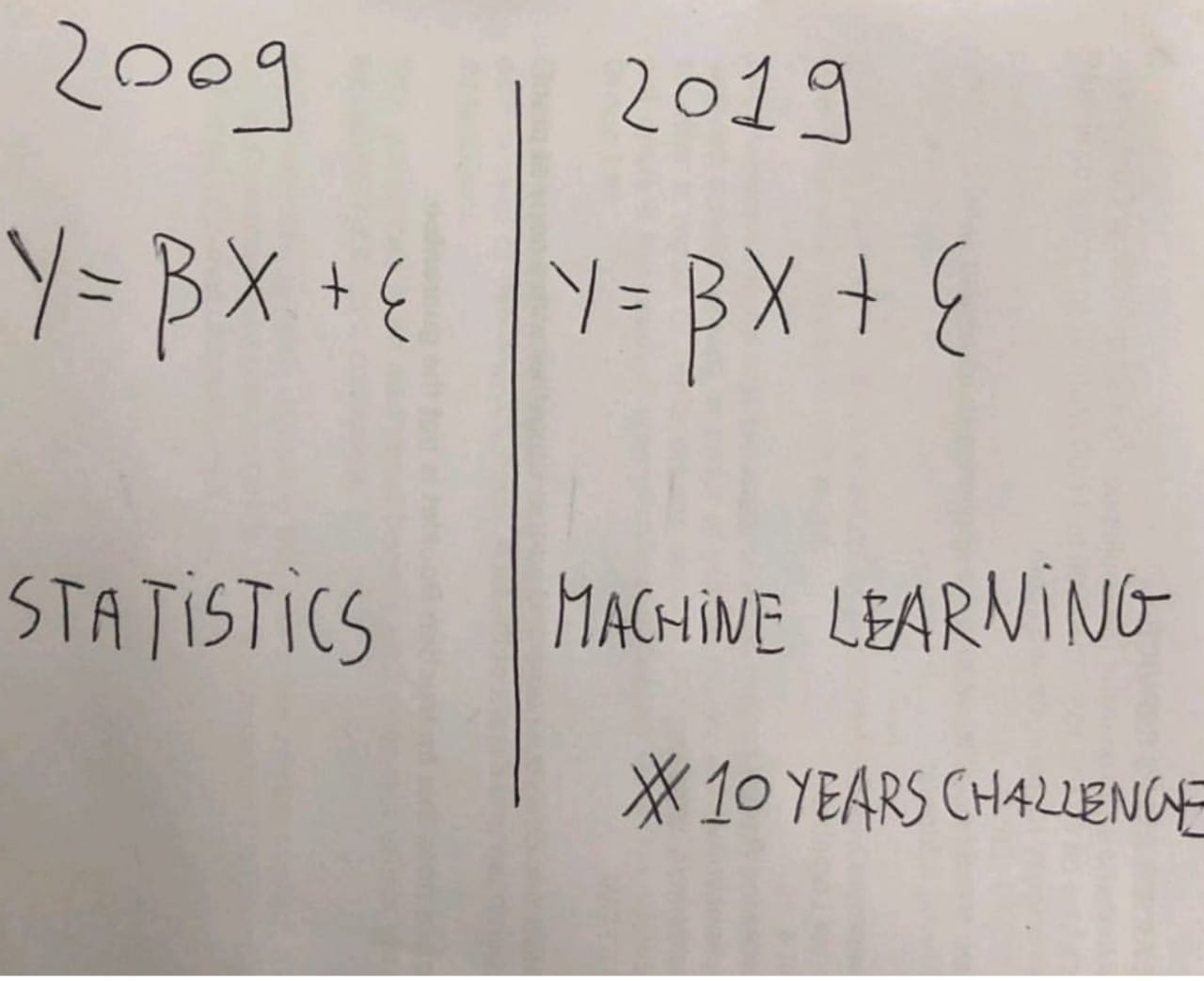

 Самые актуальные новости - в
Самые актуальные новости - в